Zadanie nr 1747421
Liczby 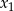 i
i 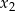 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 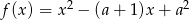 . Dla jakich
. Dla jakich 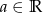 ciąg
ciąg 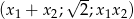 jest geometryczny?
jest geometryczny?
Rozwiązanie
Nie będziemy na razie przejmować się 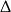 -ą – na koniec sprawdzimy ją dla otrzymanych rozwiązań. Na mocy wzorów Viète’a, mamy
-ą – na koniec sprawdzimy ją dla otrzymanych rozwiązań. Na mocy wzorów Viète’a, mamy
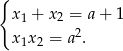
Pytamy zatem kiedy ciąg 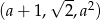 jest geometryczny. Tak będzie, gdy kwadrat środkowego wyrazu będzie iloczynem sąsiednich wyrazów czyli
jest geometryczny. Tak będzie, gdy kwadrat środkowego wyrazu będzie iloczynem sąsiednich wyrazów czyli
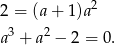
Widać, że 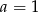 jest pierwiastkiem, dzielimy (grupując wyrazy) przez
jest pierwiastkiem, dzielimy (grupując wyrazy) przez 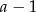 .
.
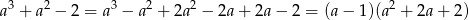
Trójmian w nawiasie nie ma pierwiastków ( ), więc musi być
), więc musi być 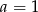 .
.
Wyjściowy trójmian ma jednak wtedy postać 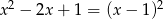 , czyli nie ma dwóch różnych pierwiastków.
, czyli nie ma dwóch różnych pierwiastków.
Odpowiedź: Nie ma takiego  .
.

