Zadanie nr 1949673
Nieskończony ciąg liczbowy 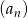 dla
dla 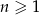 jest określony wzorem
jest określony wzorem
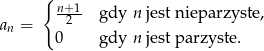
- Uzupełnij tabelkę:

1 2 3 4 5 
2005 2006 2007 2008 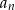
1 0 … - Oblicz
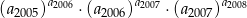 .
. - Oblicz sumę 2008 początkowych wyrazów ciągu
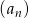 .
.
Rozwiązanie
- Tabelkę uzupełniamy wprost z definicji ciągu

1 2 3 4 5 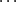
2005 2006 2007 2008 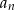
1 0 2 0 3 … 1003 0 1004 0 - Korzystamy z wyliczonych wyżej wartości
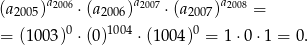
Odpowiedź: 0 - Jeszcze raz korzystając z tabelki otrzymujemy, że szukana suma jest równa
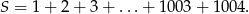
Jest to suma wyrazów ciągu arytmetycznego, więc
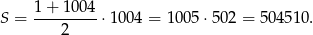
Odpowiedź: 504510

