Zadanie nr 2022442
Liczby 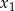 i
i 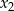 są różnymi od zera rozwiązaniami równania
są różnymi od zera rozwiązaniami równania 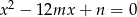 . Liczby
. Liczby 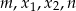 są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz
są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz 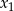 i
i 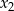 .
.
Rozwiązanie
Sprawdźmy najpierw, kiedy dane równanie ma dwa różne rozwiązania. Tak będzie, gdy
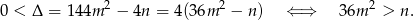
Przy tym założeniu pierwiastki danego równania spełniają wzory Viète’a
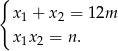
To, że liczby 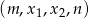 tworzą ciąg geometryczny oznacza, że
tworzą ciąg geometryczny oznacza, że
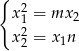
Jeżeli pomnożymy te dwa równania stronami, to mamy
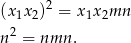
Z założenia wiemy, że 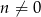 , więc mamy stąd
, więc mamy stąd 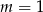 i pierwsze równanie układu przyjmuje postać
i pierwsze równanie układu przyjmuje postać
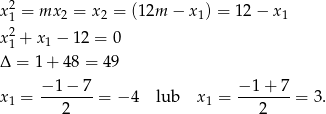
W pierwszym przypadku mamy 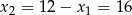 , a w drugim
, a w drugim 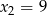 . MAmy wtedy odpowiednio
. MAmy wtedy odpowiednio 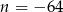 i
i 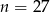 . Łatwo sprawdzić, że w obu przypadkach
. Łatwo sprawdzić, że w obu przypadkach 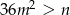 .
.
Odpowiedź: 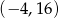 lub
lub