/Szkoła średnia/Ciągi

Zadanie nr 2111704

Dodaj do ulubionych
Dodaj do rozwiązanych

Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.

Rozwiązanie

Jeżeli oznaczymy pierwszy wyraz ciągu przez a , a iloraz przez 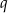q to ze wzoru 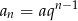an = aqn−1 na n -ty wyraz ciągu geometrycznego mamy układ równań

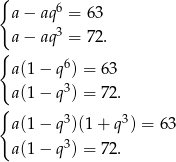
{ a− aq 6 = 63 3 { a− aq = 72. a(1− q6) = 63 a(1− q3) = 72. { 3 3 a(1− q )(1+ q ) = 63 a(1− q3) = 72.

Podstawiamy teraz 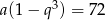a(1 − q3) = 72 z drugiego równania do pierwszego.

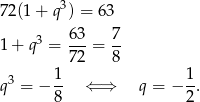
72 (1+ q 3) = 63 63 7 1 + q3 = ---= -- 72 8 q3 = − 1- ⇐ ⇒ q = − 1. 8 2

Zatem

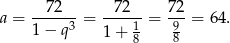
a = --72---= --72--= 72-= 64. 1− q3 1 + 18 98

Pozostało policzyć sumę pierwszych 7 wyrazów.

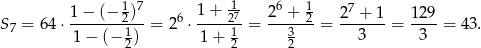
1− (− 1)7 1 + -17 26 + 1 27 + 1 129 S7 = 6 4⋅ -------21---= 26 ⋅----21-= --3--2-= ------= ----= 43. 1 − (− 2) 1 + 2 2 3 3

 
Odpowiedź: 43

Wersja PDF