Zadanie nr 2233850
Dany jest nieskończony ciąg geometryczny 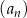 określony dla
określony dla 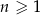 , którego wyrazy są niezerowe i iloraz
, którego wyrazy są niezerowe i iloraz 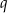 spełnia warunek:
spełnia warunek: 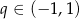 . Suma
. Suma 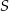 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 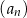 , suma
, suma 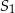 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 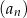 o numerach nieparzystych oraz suma
o numerach nieparzystych oraz suma 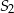 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 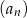 o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz
o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz 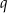 .
.
Rozwiązanie
Mamy do czynienia z trzema szeregami:
– o ilorazie 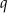 , pierwszym wyrazie
, pierwszym wyrazie 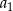 i sumie
i sumie 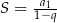
– o ilorazie 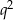 , pierwszym wyrazie
, pierwszym wyrazie 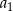 i
i 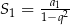
– o ilorazie 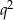 , pierwszym wyrazie
, pierwszym wyrazie 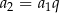 i sumie
i sumie 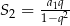 .
.
Pozostało rozwiązać równanie
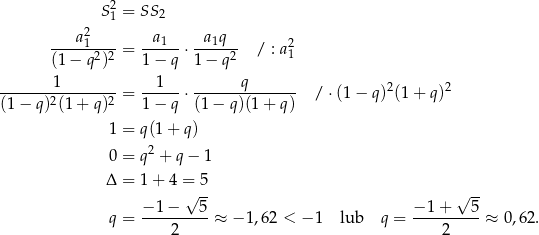
Pierwsze rozwiązanie nie spełnia warunku 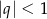 , więc
, więc 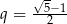 .
.
Odpowiedź: