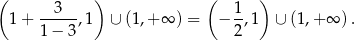/Szkoła średnia/Ciągi

Zadanie nr 2280812

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że zbiór 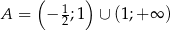( 1 ) A = − 2;1 ∪ (1;+ ∞ ) jest zbiorem wartości funkcji

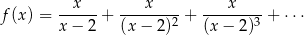
--x--- ----x---- ---x----- f(x ) = x − 2 + (x − 2 )2 + (x − 2)3 + ⋅⋅⋅

Rozwiązanie

Wyznaczmy najpierw dziedzinę funkcji 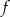f . Ze względu na mianownik musi być 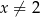x ⁄= 2 . Ponadto, iloraz 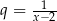q = x1−2- szeregu definiującego funkcję f musi spełniać

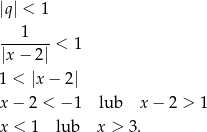
|q| < 1 1 -------< 1 |x − 2| 1 < |x− 2| x− 2 < − 1 lub x − 2 > 1 x < 1 lub x > 3 .

Przy tym założeniu funkcję możemy zapisać w postaci (korzystamy ze wzoru na sumę wszystkich wyrazów szeregu geometrycznego).

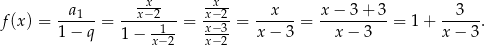
a1 x−x2 xx−2- x x− 3+ 3 3 f(x) = -----= ------1- = -x−3-= ------= ----------= 1 + ------. 1− q 1 − x− 2 x−2 x− 3 x− 3 x − 3

Wykresem tej funkcji jest hiperbola 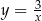y = 3 x przesunięta o 3 jednostki w prawo i jedną jednostkę do góry. Szkicujemy ten wykres.

PIC

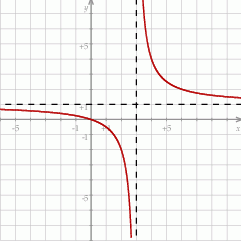
Z wykresu widać, że na zbiorze 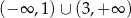(− ∞ ,1) ∪ (3,+ ∞ ) funkcja 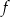f przyjmuje wartości

( ) ( ) 1 + --3---,1 ∪ 1,+ ∞ = − 1,1 ∪ 1,+ ∞ . 1 − 3 ( ) 2 ( )
Wersja PDF