/Szkoła średnia/Ciągi

Zadanie nr 2356685

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzy liczby tworzą ciąg geometryczny. Jeżeli drugą z nich zwiększymy o 8, to otrzymamy ciąg arytmetyczny. Jeżeli trzeci wyraz otrzymanego ciągu arytmetycznego zwiększymy o 64 to znów otrzymamy ciąg geometryczny. Wyznacz te liczby.

Rozwiązanie

Powiedzmy, że dane liczby to 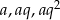2 a,aq,aq . Wiemy, że ciąg 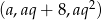2 (a,aq + 8,aq ) jest ciągiem arytmetycznym, a 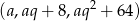(a ,aq+ 8,aq2 + 64) geometrycznym. Daje to nam równania

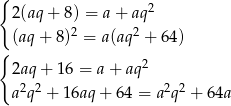
{ 2(aq+ 8) = a + aq2 2 2 { (aq+ 8) = a(aq + 64) 2aq+ 16 = a + aq2 a2q2 + 16aq + 64 = a2q 2 + 64a

Przekształćmy drugie równanie

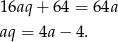
16aq + 64 = 64a aq = 4a − 4.

Podstawmy to do pierwszego równania

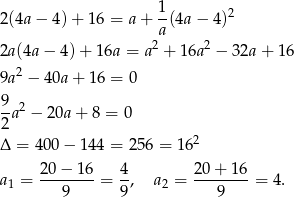
1 2(4a − 4) + 16 = a + -(4a − 4)2 2a 2 2a(4a − 4) + 16a = a + 1 6a − 32a+ 16 9a2 − 40a + 16 = 0 9- 2 2a − 20a + 8 = 0 Δ = 400− 144 = 2 56 = 162 20-−-1-6 4- 2-0+-1-6 a1 = 9 = 9 , a2 = 9 = 4.

Mamy wtedy odpowiednio

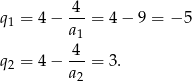
-4- q1 = 4 − a1 = 4− 9 = − 5 4 q2 = 4 − ---= 3. a2

 
Odpowiedź: 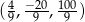(49, −290, 1090) lub (4,12,36)

Wersja PDF