/Szkoła średnia/Ciągi

Zadanie nr 2422654

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest liczba 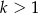k > 1 . Wyrazy ciągu 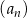(an) , określonego dla 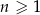n ≥ 1 , spełniają warunki

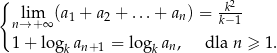
{ 2 lim (a1 + a2 + ...+ an ) = kk−1- n→ + ∞ 1 + logk an+1 = logk an, dla n ≥ 1.

Udowodnij, że

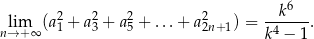
6 lim (a2 + a2+ a2+ ...+ a2 ) = --k---. n→ + ∞ 1 3 5 2n+1 k4 − 1

Rozwiązanie

Granice w sformułowaniu zadania zdają się sugerować, że mamy do czynienia z ciągiem geometrycznym. Sprawdźmy, że tak jest istotnie. Wiemy, że

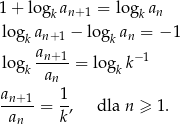
1 + logk an+1 = logk an lo g a − log an = − 1 k n+ 1 k lo g an+1-= log k−1 k an k an+1- 1- a = k, dla n ≥ 1. n

To oznacza, że faktycznie 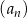(a ) n jest ciągiem geometrycznym o ilorazie 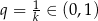1 q = k ∈ (0,1) . To z kolei oznacza, że

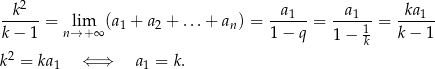
k2 a a ka ------= lim (a1 + a2 + ...+ an) = ---1--= ---1--= ---1-- k − 1 n→+ ∞ 1 − q 1− 1k k− 1 2 k = ka1 ⇐ ⇒ a1 = k.

Ciąg

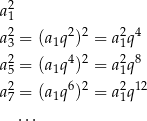
a21 2 2 2 2 4 a3 = (a1q ) = a1q a2= (a1q4)2 = a2q8 5 1 a27 = (a1q6)2 = a21q12 ...

też jest ciągiem geometrycznym, ale o pierwszym wyrazie 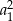2 a1 i ilorazie 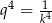q4 = 1k4 . Suma jego wyrazów jest więc równa

2 2 2 2 2 --a1-- -k2-- --k6-- nli→m+ ∞(a1 + a3 + a5 + ...+ a2n+ 1) = 1 − -1 = k4−-1 = k4 − 1 . k4 k4
Wersja PDF