Zadanie nr 2580893
Dany jest ciąg geometryczny 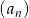 , określony dla
, określony dla 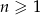 , w którym spełniona jest równość
, w którym spełniona jest równość 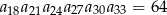 . Oblicz iloczyn
. Oblicz iloczyn 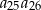 .
.
Rozwiązanie
Oznaczmy przez 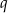 iloraz ciągu
iloraz ciągu 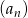 . Ze wzoru na
. Ze wzoru na  -ty wyraz ciągu geometrycznego mamy
-ty wyraz ciągu geometrycznego mamy
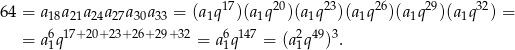
Stąd 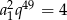 i
i
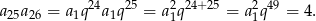
Odpowiedź: 4
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest ciąg geometryczny 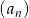 , określony dla
, określony dla 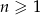 , w którym spełniona jest równość
, w którym spełniona jest równość 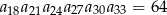 . Oblicz iloczyn
. Oblicz iloczyn 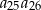 .
.
Oznaczmy przez 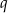 iloraz ciągu
iloraz ciągu 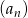 . Ze wzoru na
. Ze wzoru na  -ty wyraz ciągu geometrycznego mamy
-ty wyraz ciągu geometrycznego mamy
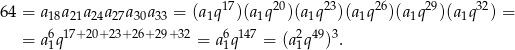
Stąd 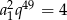 i
i
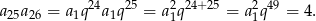
Odpowiedź: 4
