Zadanie nr 2609277
Pierwszy wyraz malejącego ciągu arytmetycznego 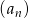 jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu
jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu 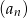 oraz sumę 14 jego początkowych wyrazów.
oraz sumę 14 jego początkowych wyrazów.
Rozwiązanie
Wyraz ogólny ciągu arytmetycznego to 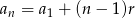 . W szczególności
. W szczególności 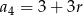 i
i 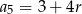 . Otrzymujemy zatem równanie
. Otrzymujemy zatem równanie
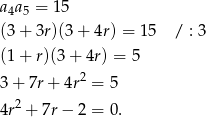
Liczymy 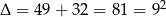 . Stąd
. Stąd
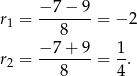
Ponieważ ciąg ma być malejący,  musi być ujemne. Zatem
musi być ujemne. Zatem 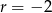 .
.
Aby obliczyć sumę 14 początkowych wyrazów, korzystamy ze wzoru
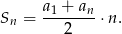
W naszej sytuacji
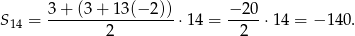
Odpowiedź: Różnica: 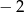 , suma:
, suma: 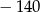 .
.

