Zadanie nr 2647953
W ciągu arytmetycznym 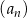 , określonym dla
, określonym dla 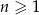 , suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę
, suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę 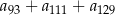 .
.
Rozwiązanie
Korzystamy ze wzoru 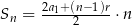 na sumę
na sumę  początkowych wyrazów ciągu arytmetycznego.
początkowych wyrazów ciągu arytmetycznego.
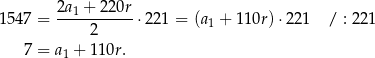
Mamy zatem
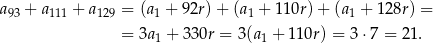
Odpowiedź: 21
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W ciągu arytmetycznym 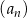 , określonym dla
, określonym dla 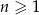 , suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę
, suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę 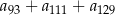 .
.
Korzystamy ze wzoru 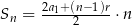 na sumę
na sumę  początkowych wyrazów ciągu arytmetycznego.
początkowych wyrazów ciągu arytmetycznego.
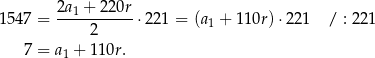
Mamy zatem
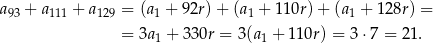
Odpowiedź: 21
