Zadanie nr 2651802
Ciąg 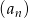 dany jest wzorem
dany jest wzorem 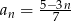 , dla
, dla 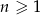 .
.
- Oblicz sumę
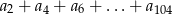 .
. - Ustalmy
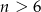 . Dla jakich
. Dla jakich  liczby
liczby 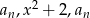 są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Rozwiązanie
- Ze wzoru ciągu
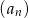 widać, że jest to ciąg arytmetyczny (bo każdy ciąg postaci
widać, że jest to ciąg arytmetyczny (bo każdy ciąg postaci 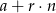 jest ciągiem arytmetycznym), ale dla pewności sprawdźmy to. Liczymy różnicę dwóch kolejnych wyrazów
jest ciągiem arytmetycznym), ale dla pewności sprawdźmy to. Liczymy różnicę dwóch kolejnych wyrazów 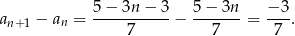
Skoro różnica jest stała (nie zależy od
 ), ciąg jest arytmetyczny.
), ciąg jest arytmetyczny. Liczby
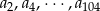 również będą tworzyły ciąg arytmetyczny, ale o dwa razy większej różnicy
również będą tworzyły ciąg arytmetyczny, ale o dwa razy większej różnicy 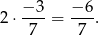
Możemy więc policzyć żądaną sumę ze wzoru: pierwszy+ostatni przez dwa razy liczba wyrazów. Wyrazów jest 52 (połowa liczb od 1 do 104), więc suma jest równa
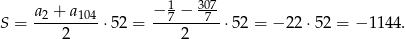
Odpowiedź: -1144 - Trzy liczby
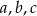 są kolejnymi wyrazami ciągu geometrycznego jeżeli
są kolejnymi wyrazami ciągu geometrycznego jeżeli 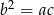 . Daje to nam równanie
. Daje to nam równanie 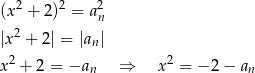
Wartość bezwzględną opuściliśmy korzystając z tego, że
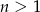 , czyli
, czyli 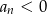 . Ponieważ
. Ponieważ 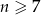 , mamy ponadto
, mamy ponadto 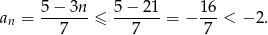
Zatem
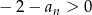 i mamy
i mamy 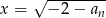 lub
lub 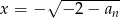 .
.
Odpowiedź: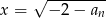 lub
lub 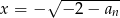 .
.

