/Szkoła średnia/Ciągi

Zadanie nr 2679427

Dodaj do ulubionych
Dodaj do rozwiązanych

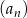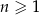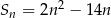Suma n początkowych wyrazów ciągu (an) dla każdego n ≥ 1 określona jest wzorem Sn = 2n2 − 14n .

  • Wykaż, że ciąg 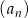(an) jest ciągiem arytmetycznym.
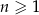  • Wykaż, że jeżeli suma n początkowych wyrazów ciągu dla każdego n ≥ 1 określona jest wzorem 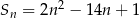2 Sn = 2n − 1 4n + 1 , to ciąg ten nie jest arytmetyczny.
  • Znajdź takie trzy kolejne wyrazy ciągu 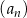(an) , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.

Rozwiązanie

  • Zauważmy, że mając wzór na sumę ciągu, łatwo jest wyznaczyć wzór na jego wyraz ogólny an .
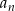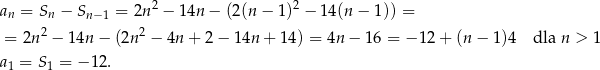
    an = Sn − Sn− 1 = 2n2 − 14n − (2 (n− 1)2 − 14(n − 1)) = 2 2 = 2n − 14n − (2n − 4n + 2− 14n + 14) = 4n − 16 = − 12 + (n − 1)4 dla n > 1 a = S = − 12. 1 1

    No i widać, że mamy ciąg arytmetyczny o pierwszym wyrazie -12 i różnicy 4. Jeżeli jednak nie jesteśmy tego pewni, to wystrczy sprawdzić czy różnica między dwoma kolejnymi wyrazami jest stała (nie zależy od n ). Liczymy

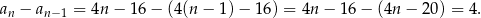
    a − a = 4n − 16 − (4 (n − 1)− 16) = 4n − 16 − (4n − 20) = 4. n n− 1
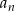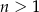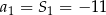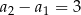  • Wyliczenie an dla n > 1 jest dokładnie takie samo jak poprzednio. To co się nie zgadza, to pierwszy wyraz. Mamy a1 = S 1 = − 11 i a2 − a1 = 3 , pomimo, że 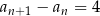an+1 − an = 4 dla n > 1 .
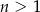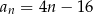  • Mamy dwie możliwości na kolejność, w której będziemy odejmować sąsiednie wyrazy, to prowadzi do dwóch równań. Zajmijmy się pierwszym z nich (z pierwszego podpunktu wiemy, że an = 4n − 16 )
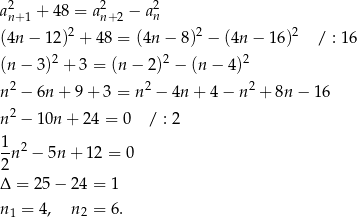
    a2n+1 + 48 = a2n+2 − a2n 2 2 2 (4n − 12) + 48 = (4n − 8) − (4n − 16) / : 16 (n − 3)2 + 3 = (n − 2)2 − (n − 4)2 2 2 2 n − 6n + 9 + 3 = n − 4n + 4− n + 8n − 16 n2 − 10n + 2 4 = 0 / : 2 1-n2 − 5n + 12 = 0 2 Δ = 25− 24 = 1 n1 = 4 , n2 = 6.

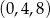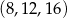    Daje to nam trójki wyrazów (0,4,8) i (8,1 2,16) .

    Pozostało rozpatrzyć drugą możliwość.

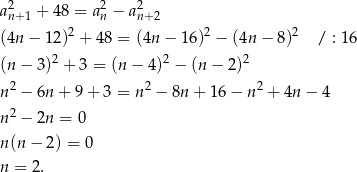
    a2 + 48 = a2n − a2 n+1 2 n+2 2 2 (4n − 12) + 48 = (4n − 16) − (4n − 8) / : 16 (n − 3)2 + 3 = (n − 4)2 − (n − 2)2 n2 − 6n + 9 + 3 = n2 − 8n + 16 − n2 + 4n − 4 2 n − 2n = 0 n(n − 2 ) = 0 n = 2 .

    daje to nam trójkę (− 8,− 4,0) .

 
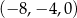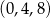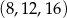Odpowiedź: (0,4,8) lub (8,12,1 6) lub (− 8,− 4,0)

Wersja PDF