/Szkoła średnia/Ciągi

Zadanie nr 2753946

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są dwa ciągi rosnące: arytmetyczny 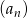(an) i geometryczny 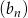(bn) . Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.

Rozwiązanie

Oznaczając iloraz ciągu geometrycznego przez 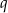q , a różnicę ciągu arytmetycznego przez r , mamy układ równań

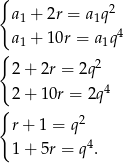
{ a1 + 2r = a1q2 a + 10r = a q 4 { 1 1 2 + 2r = 2q 2 4 2 + 10r = 2q { 2 r + 1 = q 1 + 5r = q4.

Sposób I

Podstawiając r z pierwszego równania do drugiego, mamy

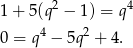
1+ 5(q2 − 1) = q4 4 2 0 = q − 5q + 4.

Jest to równanie dwukwadratowe, więc podstawiamy 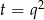t = q2 .

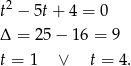
2 t − 5t+ 4 = 0 Δ = 25− 16 = 9 t = 1 ∨ t = 4.

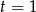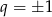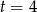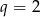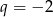t = 1 prowadzi do q = ± 1 , co jest niemożliwe, bo ciąg geometryczny ma być rosnący. Zatem t = 4 i q = 2 (q = − 2 nie daje ciągu rosnącego). Stąd 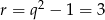r = q2 − 1 = 3 . Zatem

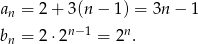
an = 2+ 3(n − 1) = 3n − 1 n−1 n bn = 2⋅2 = 2 .

Sposób II

Tym razem podstawmy 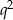q 2 pierwszego równania do drugiego.

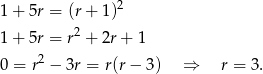
2 1 + 5r = (r + 1) 1 + 5r = r2 + 2r+ 1 0 = r2 − 3r = r(r − 3) ⇒ r = 3.

Rozwiązanie 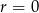r = 0 odrzuciliśmy, bo ciąg arytmetyczny ma być rosnący. Stąd

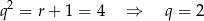
q2 = r + 1 = 4 ⇒ q = 2

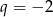(q = − 2 nie daje ciągu rosnącego). Wzory ciągów wyznaczamy jak poprzednio.  
Odpowiedź: an = 3n − 1, b = 2n

Wersja PDF