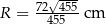Zadanie nr 2862662
W trójkącie dwa boki mają długość 3 cm i 4 cm. Długość trzeciego boku jest większa od długości dwóch pozostałych boków. Długości wysokości w tym trójkącie są trzema kolejnymi wyrazami ciągu arytmetycznego. Oblicz pole tego trójkąta oraz długości promieni okręgów: wpisanego w ten trójkąt i opisanego na tym trójkącie.
Rozwiązanie
Ponieważ iloczyn długości boku i opuszczonej na niego wysokości jest równy podwojonemu polu  trójkąta, więc jeżeli oznaczymy przez
trójkąta, więc jeżeli oznaczymy przez 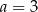 ,
, 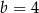 i
i  boki trójkąta oraz
boki trójkąta oraz 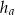 ,
, 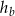 i
i 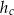 opuszczone na nie wysokości, to
opuszczone na nie wysokości, to 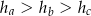 .
.
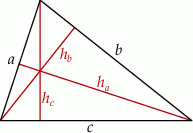
Zatem z informacji o tym, że liczby 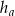 ,
, 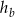 i
i 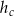 tworzą ciąg arytmetyczny mamy
tworzą ciąg arytmetyczny mamy
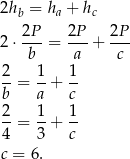
Pole trójkąta możemy obliczyć ze wzoru Herona.
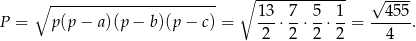
Promienie okręgów wpisanego i opisanego możemy wyliczyć ze wzorów na pole 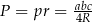 .
.
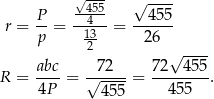
Odpowiedź: 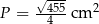 ,
, 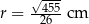 ,
,