/Szkoła średnia/Ciągi

Zadanie nr 2865374

Dodaj do ulubionych
Dodaj do rozwiązanych

W ciągu geometrycznym 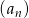(an) , określonym dla 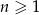n ≥ 1 , dane są: wyraz 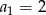a1 = 2 i suma trzech początkowych wyrazów tego ciągu 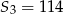S3 = 11 4 . Wiadomo ponadto, że 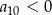a10 < 0 . Oblicz iloraz

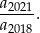
a -2021. a2018

Rozwiązanie

Jeżeli oznaczymy przez 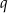q iloraz danego ciągu, to z podanej sumy mamy

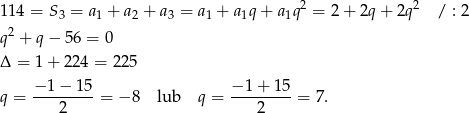
2 2 114 = S3 = a1 + a2 + a3 = a1 + a1q+ a1q = 2 + 2q + 2q / : 2 q2 + q− 56 = 0 Δ = 1+ 224 = 22 5 −-1-−-15- −-1-+-15- q = 2 = − 8 lub q = 2 = 7.

Ponieważ ciąg ma mieć wyrazy ujemne, mamy stąd 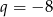q = − 8 i

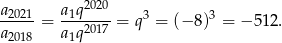
a a q2020 -2021-= -1----- = q3 = (− 8)3 = −5 12. a2018 a1q2017

 
Odpowiedź: − 512

Wersja PDF