Zadanie nr 3029556
Długości boków trapezu prostokątnego tworzą ciąg geometryczny. Ramię, które jest najkrótszym bokiem trapezu ma długość 1. Krótsza podstawa trapezu jest krótsza od drugiego z ramion. Oblicz długość dłuższej podstawy.
Rozwiązanie
Szkicujemy trapez.
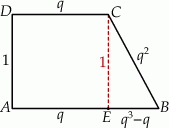
Ponieważ długości boków trapezu tworzą ciąg geometryczny, to możemy je oznaczyć przez 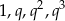 dla pewnego
dla pewnego 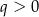 . Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym
. Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym 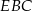 .
.
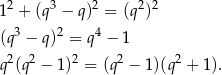
Zauważmy teraz, że jeżeli 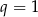 , to trapez jest kwadratem i nie spełnia opisu podanego w treści zadania. W takim razie
, to trapez jest kwadratem i nie spełnia opisu podanego w treści zadania. W takim razie 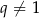 i możemy powyższe równanie podzielić przez
i możemy powyższe równanie podzielić przez 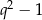 . Pozostanie równanie
. Pozostanie równanie
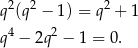
Podstawmy 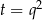 .
.
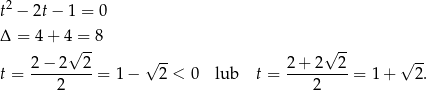
Ujemne rozwiązanie odrzucamy i mamy 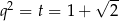 , czyli
, czyli 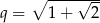 . Stąd
. Stąd
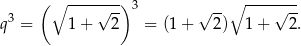
Odpowiedź: