/Szkoła średnia/Ciągi

Zadanie nr 3169907

Dodaj do ulubionych
Dodaj do rozwiązanych

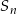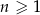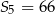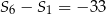W ciągu geometrycznym przez Sn oznaczamy sumę n początkowych wyrazów tego ciągu, dla liczb naturalnych n ≥ 1 . Wiadomo, że dla pewnego ciągu geometrycznego: S5 = 66 i S6 − S1 = − 33 . Wyznacz iloraz i ósmy wyraz tego ciągu.

Rozwiązanie

Wiemy, że

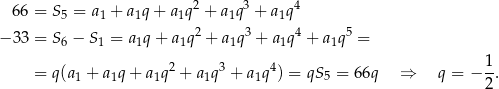
2 3 4 6 6 = S5 = a1 + a1q + a1q + a1q + a1q −3 3 = S6 − S1 = a1q + a1q 2 + a1q3 + a1q4 + a1q5 = = q(a1 + a1q+ a1q2 + a1q3 + a1q4) = qS5 = 6 6q ⇒ q = − 1-. 2

Stąd

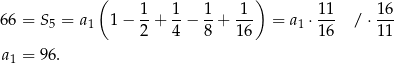
( ) 1- 1- 1- -1- 11- 16- 66 = S 5 = a1 1− 2 + 4 − 8 + 16 = a1 ⋅ 16 / ⋅ 11 a1 = 96 .

Mamy zatem

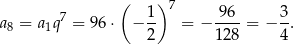
( ) 7 7 1- -96- 3- a8 = a1q = 96 ⋅ − 2 = − 12 8 = − 4 .

 
Odpowiedź: 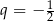1 q = − 2 , 3 a8 = − 4

Wersja PDF