/Szkoła średnia/Ciągi

Zadanie nr 3650025

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód trapezu równoramiennego wynosi 116. Oblicz pole tego trapezu, jeśli długości ramienia i podstaw trapezu są (w podanej kolejności) trzema kolejnymi wyrazami ciągu arytmetycznego oraz długość odcinka łączącego środki ramion trapezu wynosi 41.

Rozwiązanie

Zacznijmy od rysunku.

PIC

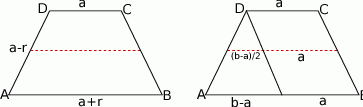
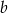Będziemy korzystać z dość dobrze znanej własności, że odcinek łączący środki ramion trapezu o podstawach a i b ma długość 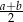a+b- 2 – uzasadnienie tej równości łatwo odczytać z prawego rysunku.

Jeżeli oznaczymy boki trapezu przez 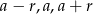a − r,a,a + r , to z powyższej uwagi mamy

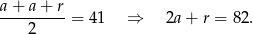
a+ a+ r ---------= 41 ⇒ 2a + r = 82. 2

Warunek z obwodem daje nam

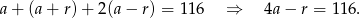
a + (a + r)+ 2(a− r) = 116 ⇒ 4a − r = 116.

Daje to nam układ równań

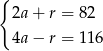
{ 2a+ r = 82 4a− r = 116

Dodajemy te równania stronami (żeby skrócić r ) i mamy

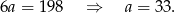
6a = 19 8 ⇒ a = 33.

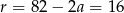Zatem r = 82 − 2a = 16 i boki trapezu wynoszą 17,33,49.

Aby obliczyć pole trapezu, musimy obliczyć jego wysokość.

PIC

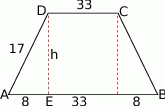
W tym celu patrzymy na trójkąt prostokątny 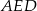AED .

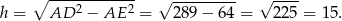
∘ ------------ √ --------- √ ---- h = AD 2 − AE 2 = 289 − 6 4 = 225 = 15.

Zatem pole jest równe

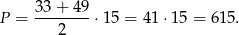
P = 3-3+-4-9⋅ 15 = 41 ⋅15 = 6 15. 2

 
Odpowiedź: 615

Wersja PDF