/Szkoła średnia/Ciągi

Zadanie nr 3682965

Dodaj do ulubionych
Dodaj do rozwiązanych

Monotoniczny ciąg geometryczny 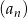(an) jest zdefiniowany przez warunki

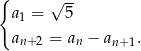
{ √ -- a1 = 5 an+ 2 = an − an+1.

Oblicz sumę wszystkich wyrazów ciągu 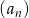(a ) n .

Rozwiązanie

Jeżeli oznaczymy przez 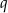q iloraz ciągu 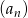(an) , to mamy 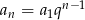n− 1 an = a1q i dany warunek rekurencyjny przyjmuje postać.

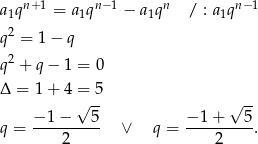
n+ 1 n− 1 n n− 1 a1q = a1q − a1q / : a1q q2 = 1 − q q2 + q − 1 = 0 Δ = 1 + 4 = 5 √ -- √ -- − 1− 5 − 1+ 5 q = ----2----- ∨ q = ----2----.

Ponieważ ciąg ma być monotoniczny, pierwsze rozwiązanie odrzucamy i mamy

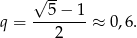
-- √ 5 − 1 q = --------≈ 0,6. 2

Ponieważ 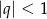|q| < 1 , możemy obliczyć sumę wszystkich wyrazów ciągu (an) .

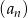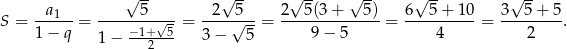
√ -- √ -- √ -- √ -- √ -- √ -- S = -a1--= ------5-√-- = --2-√5--= 2--5(3-+---5-)= 6--5-+-10-= 3--5-+-5-. 1− q 1 − −-1+--5 3 − 5 9 − 5 4 2 2

 
Odpowiedź: √ - 3--5+5 2

Wersja PDF