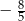/Szkoła średnia/Ciągi

Zadanie nr 3753570

Dodaj do ulubionych
Dodaj do rozwiązanych

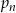Niech pn , dla liczby całkowitej 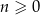n ≥ 0 , oznacza sumę odwrotności pierwiastków równania

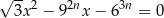
√ -- 3x2 − 92nx − 63n = 0

z niewiadomą x . Oblicz sumę wszystkich wyrazów ciągu (pn ) .

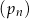Rozwiązanie

Zauważmy najpierw, że

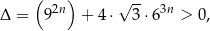
( 2n) √ -- 3n Δ = 9 + 4 ⋅ 3⋅6 > 0,

więc dane równie ma zawsze dwa pierwiastki rzeczywiste i na mocy wzorów Viète’a mamy

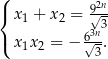
( { 9√2n- x1 + x2 = 3 ( x1x 2 = − 6√3n. 3

Stąd

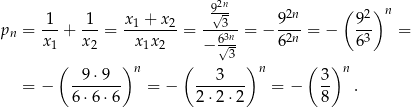
92n ( ) 1 1 x1 + x2 √3- 92n 92 n pn = x--+ x--= -x-x----= --63n-= − 62n-= − 63- = 1 2 1 2 − √3 ( 9⋅ 9 )n ( 3 )n ( 3)n = − ------- = − ------- = − -- . 6 ⋅6 ⋅6 2⋅2 ⋅2 8

Jest to więc ciąg geometryczny o pierwszym wyrazie 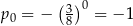( )0 p0 = − 38 = − 1 i ilorazie 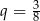q = 3 8 . Suma tego ciągu jest więc równa

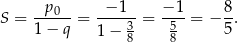
--p0-- -−-1-- −-1- 8- S = 1 − q = 1 − 3 = 5 = − 5 . 8 8

 
Odpowiedź: 8 − 5

Wersja PDF