/Szkoła średnia/Ciągi

Zadanie nr 3852651

Dodaj do ulubionych
Dodaj do rozwiązanych

Ciąg geometryczny 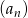(an) jest określony wzorem 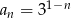1−n an = 3 dla n ≥ 1 .

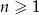  • Oblicz iloraz tego ciągu.
  • Oblicz 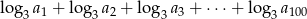log a + log a + log a + ⋅⋅⋅+ log a 3 1 3 2 3 3 3 100 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.

Rozwiązanie

  • Iloraz to iloraz dwóch sąsiednich wyrazów:
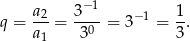
    a2- 3−1- −1 1- q = a = 3 0 = 3 = 3. 1

     
    Odpowiedź: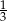 13

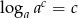  • Prosty rachunek (pod warunkiem znajmości wzoru log ac = c a ):
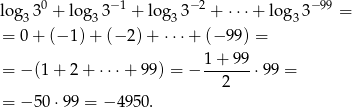
    lo g 30 + log 3−1 + log 3 −2 + ⋅⋅⋅+ log 3− 99 = 3 3 3 3 = 0 + (− 1) + (− 2) + ⋅⋅⋅+ (− 99) = 1 + 9 9 = − (1 + 2 + ⋅⋅⋅ + 99) = − -------⋅ 99 = 2 = − 50 ⋅99 = − 4950.

    Pod koniec wykorzystaliśmy wzór na sumę wyrazów ciągu arytmetycznego.

 
Odpowiedź: -4950

Wersja PDF