/Szkoła średnia/Ciągi

Zadanie nr 3894786

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź wartość parametru 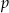p , dla której granica ciągu 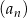(an) określonego wzorem

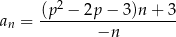
2 a = (p--−-2p-−--3)n-+-3 n −n

jest równa 4. Zbadaj monotoniczność ciągu 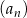(an) dla znalezionej wartości p .

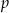Rozwiązanie

Spróbujmy obliczyć granicę ciągu 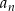an .

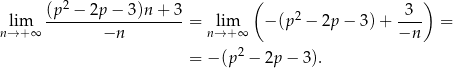
2 ( ) lim (p--−-2p-−-3-)n+--3 = lim − (p2 − 2p − 3) + --3- = n→ +∞ −n n→ +∞ −n = − (p2 − 2p − 3 ).

Mamy zatem równanie

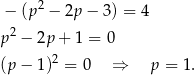
2 − (p − 2p − 3) = 4 2 p − 2p + 1 = 0 (p− 1)2 = 0 ⇒ p = 1.

Dany ciąg ma zatem wzór

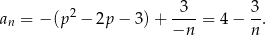
2 -3-- 3- an = − (p − 2p − 3) + −n = 4 − n .

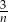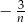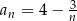Ciąg 3 n jest malejący, więc ciąg − 3 n jest rosnący. Zatem rosnący jest też ciąg 3 an = 4− n .  
Odpowiedź: 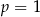p = 1 , rosnący.

Wersja PDF