Zadanie nr 3941431

Ciąg 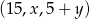(1 5,x,5 + y) jest arytmetyczny, natomiast ciąg 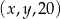(x,y,20) jest geometryczny. Oblicz oraz 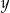i podaj ten ciąg geometryczny.

Rozwiązanie

Jeżeli liczby 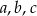a,b,c są kolejnymi wyrazami ciągu arytmetycznego to 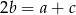2b = a+ c . Jeżeli są kolejnymi wyrazami ciągu geometrycznego to 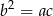b2 = ac . Mamy zatem układ równań

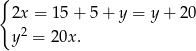
{ 2x = 15 + 5+ y = y + 20 2 y = 20x.

Podstawiając wartość 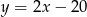y = 2x − 20 z pierwszego równania do drugiego mamy

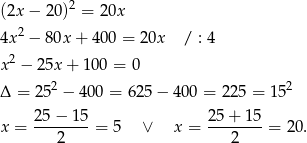
(2x − 20)2 = 20x 2 4x − 80x + 4 00 = 20x / : 4 x2 − 25x + 10 0 = 0 2 2 Δ = 25 − 400 = 6 25− 400 = 22 5 = 15 25− 15 25 + 1 5 x = --------= 5 ∨ x = -------- = 20. 2 2

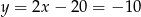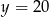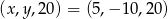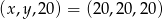Mamy wtedy odpowiednio y = 2x − 20 = − 10 i y = 20 , co daje dwa ciągi (x,y ,20) = (5,− 10,20 ) i (x ,y,20) = (20 ,2 0,20) .
Odpowiedź: 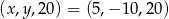(x,y ,2 0) = (5,− 10,20) lub (x,y ,20) = (20,20 ,2 0)