/Szkoła średnia/Ciągi

Zadanie nr 3947344

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczby dodatnie 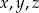x,y ,z są wyrazami ciągu geometrycznego o numerach równych odpowiednio 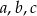a,b,c , a liczby 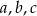a,b,c są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że

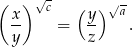
( ) √- √- x c ( y) a -- = -- . y z

Rozwiązanie

Wiemy, że

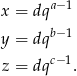
a− 1 x = dq y = dqb− 1 c− 1 z = dq .

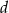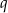dla pewnych liczb d i q . Wiemy ponadto, że

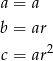
a = a b = ar 2 c = ar

dla pewnej liczby r . Mamy zatem

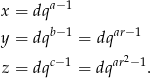
x = dqa− 1 b− 1 ar−1 y = dq = dq z = dqc− 1 = dqar2− 1.

Podstawiamy teraz te wyrażenia do równości, którą mamy udowodnić.

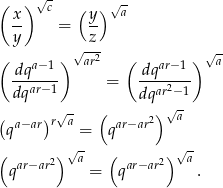
( ) √c ( )√ - x- = y- a y z ( ) √ar2- ( ) √a- dqa−-1- dqar−-1- dqar−1 = dqar2−1 √- ( ) √- ( a−ar)r a ar−ar2 a q = q ( 2)√a- ( 2)√a qar−ar = qar−ar .

Otrzymana równość jest oczywiście prawdziwa, więc wyjściowa równość też musiała być spełniona.

Wersja PDF