Zadanie nr 4078121
Ciąg 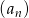 , dla
, dla 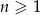 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 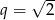 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
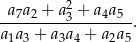
Rozwiązanie
Korzystając ze wzoru na  -ty wyraz ciągu geometrycznego, mamy
-ty wyraz ciągu geometrycznego, mamy
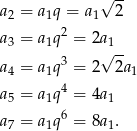
Sposób I
Podane wyrażenie jest równe
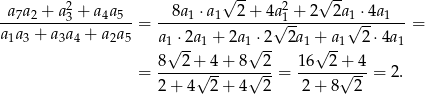
Sposób II
Tym razem wstrzymamy się ze wstawianiem wartości 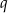 do samego końca rachunku.
do samego końca rachunku.
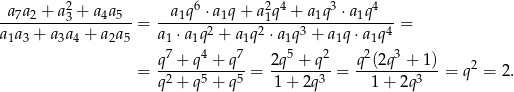
Odpowiedź: 2

