Zadanie nr 4283838
W rosnącym ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego równa się 7, a suma kwadratów wyrazów drugiego i czwartego równa się 40. Wyznacz pierwszy wyraz tego ciągu.
Rozwiązanie
Jeżeli oznaczymy pierwszy wyraz ciągu przez 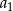 , a jego różnicę przez
, a jego różnicę przez  , to z pierwszej informacji mamy równanie
, to z pierwszej informacji mamy równanie
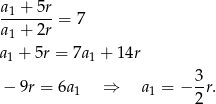
Teraz zapiszmy drugi warunek.
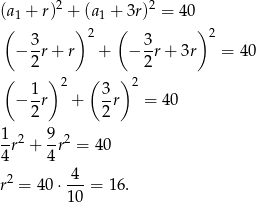
Ponieważ ciąg ma być rosnący, więc musi być 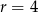 (
( musi być dodatnie). Stąd
musi być dodatnie). Stąd
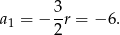
Odpowiedź: