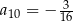/Szkoła średnia/Ciągi

Zadanie nr 4285236

Dodaj do ulubionych
Dodaj do rozwiązanych

W ciągu geometrycznym 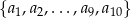{a1,a2,...,a9,a10} iloczyn wyrazów o numerach parzystych jest równy 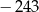− 243 , a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.

Rozwiązanie

Korzystamy ze wzoru 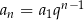n−1 an = a 1q na n –ty wyraz ciągu geometrycznego.

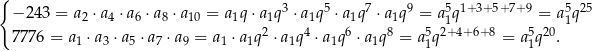
{ 3 5 7 9 5 1+ 3+5+7+ 9 5 25 − 243 = a2 ⋅a4 ⋅ a6 ⋅a8 ⋅a10 = a1q ⋅a1q ⋅ a1q ⋅a1q ⋅a1q = a1q = a1q 7776 = a 1 ⋅a3 ⋅a5 ⋅a 7 ⋅a9 = a1 ⋅a1q2 ⋅a1q4 ⋅a 1q6 ⋅a1q8 = a51q2+4+6+ 8 = a51q20.

Dzielimy teraz pierwsze równanie przez drugie i mamy

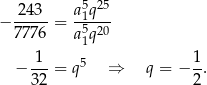
5 25 − 24-3-= a1q-- 7776 a5q20 1 − -1-= q5 ⇒ q = − 1-. 32 2

Wracamy teraz raz jeszcze do drugiego równania układu

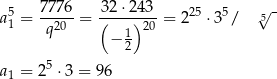
7 776 32 ⋅243 √ - a51 = --20- = (---)-20 = 225 ⋅3 5/ 5 q − 1 2 a1 = 25 ⋅3 = 96

Zatem

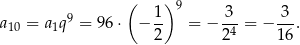
( 1 ) 9 3 3 a10 = a 1q 9 = 96⋅ − -- = − -4-= − --. 2 2 16

 
Odpowiedź: -3 a10 = − 16

Wersja PDF