/Szkoła średnia/Ciągi

Zadanie nr 4523817

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzy liczby 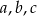a,b,c których suma jest równa 15, tworzą w tej kolejności ciąg arytmetyczny. Jeśli do pierwszej z tych liczb dodać 2, od drugiej odjąć 1, a trzecią podzielić przez 2, to tak otrzymane liczby (w tej kolejności) utworzą ciąg geometryczny malejący. Wyznacz iloraz tego ciągu geometrycznego.

Rozwiązanie

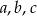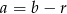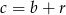Ponieważ a,b,c tworzą ciąg arytmetyczny, więc a = b − r i c = b + r dla pewnego r . Z podanej sumy mamy więc

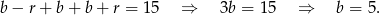
b − r+ b+ b+ r = 15 ⇒ 3b = 1 5 ⇒ b = 5.

Szukamy zatem liczb postaci 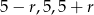5 − r,5,5 + r . Liczby 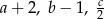c a+ 2, b − 1, 2 tworzą ciąg geometryczny, więc

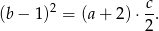
c (b − 1)2 = (a + 2) ⋅-. 2

Podstawiamy wcześniej uzyskane wyniki i otrzymujemy

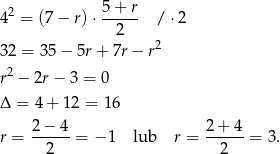
5+ r 42 = (7 − r)⋅ ----- / ⋅2 2 2 32 = 35 − 5r + 7r − r 2 r − 2r − 3 = 0 Δ = 4+ 12 = 16 2 − 4 2 + 4 r = ------= − 1 lub r = ------= 3 . 2 2

Ponieważ liczby 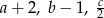c a+ 2, b − 1 ,2 mają tworzyć malejący ciąg geometryczny musimy mieć 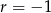r = − 1 . Otrzymujemy wtedy liczby 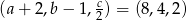c (a + 2,b − 1, 2) = (8,4,2) . Oczywiście jest to ciąg o ilorazie q = 12 .  
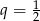Odpowiedź: 1 2

Wersja PDF