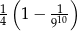/Szkoła średnia/Ciągi

Zadanie nr 4535770

Dodaj do ulubionych
Dodaj do rozwiązanych

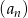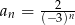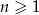Dwudziestowyrazowy ciąg geometryczny (an) określony jest wzorem an = (−23)n dla n ≥ 1 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.

Rozwiązanie

Wypiszmy kilka początkowych wyrazów ciągu 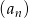(an)

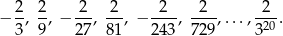
2 2 2 2 2 2 2 − -, -, − --, ---, −----, ---,..., -20. 3 9 27 81 24 3 729 3

Widać, że mamy do czynienia z ciągiem geometrycznym o ilorazie 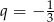1 q = − 3 , więc co drugi wyraz ciągu jest dodatni. Musimy zatem obliczyć sumę

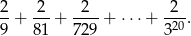
2-+ -2-+ -2--+ ⋅ ⋅⋅+ -2- . 9 8 1 729 3 20

Jest to suma 10 wyrazów ciągu geometrycznego o ilorazie 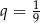1 q = 9 i pierwszym wyrazie równym 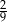29 . Korzystamy ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego.

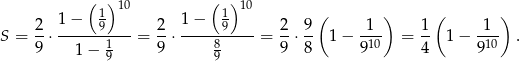
( 1) 10 ( 1)10 ( ) ( ) 2- 1-−---9--- 2- 1-−---9--- 2- 9- 1-- 1- 1-- S = 9 ⋅ 1− 1 = 9 ⋅ 8 = 9 ⋅8 1 − 910 = 4 1 − 910 . 9 9

 
Odpowiedź: ( ) 1 1 − -1- 4 910

Wersja PDF