/Szkoła średnia/Ciągi

Zadanie nr 4551910

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz sumę ośmiu początkowych wyrazów rosnącego ciągu geometrycznego, w którym 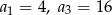a1 = 4, a3 = 16 .

Rozwiązanie

Wyliczmy najpierw 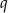q .

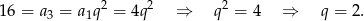
2 2 2 16 = a 3 = a1q = 4q ⇒ q = 4 ⇒ q = 2.

Powyżej skorzystaliśmy z informacji o tym, że ciąg jest rosnący, czyli 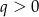q > 0 . Zatem ze wzoru na sumę wyrazów ciągu geometrycznego, mamy

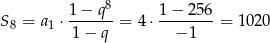
8 1−--q-- 1-−-256- S 8 = a1 ⋅ 1 − q = 4 ⋅ − 1 = 1020

 
Odpowiedź: 1020

Wersja PDF