/Szkoła średnia/Ciągi

Zadanie nr 4701050

Dodaj do ulubionych
Dodaj do rozwiązanych

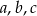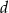Udowodnij, że jeżeli cztery liczby dodatnie a,b ,c i d są kolejnymi wyrazami ciągu geometrycznego, to a+ d ≥ b + c .

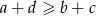Rozwiązanie

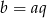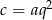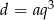Wiemy, że b = aq , 2 c = aq i 3 d = aq . Przekształćmy podaną nierówność.

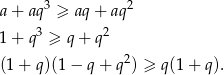
3 2 a+ aq ≥ aq+ aq 1+ q3 ≥ q+ q2 2 (1+ q)(1− q+ q ) ≥ q(1+ q).

Chcemy teraz podzielić przez 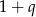1+ q . Możemy to zrobić, bo wiemy, że liczby 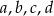a,b,c,d są dodatnie, więc q > 0 .

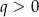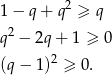
1 − q + q2 ≥ q 2 q − 2q + 1 ≥ 0 (q − 1)2 ≥ 0 .

Otrzymana nierówność jest oczywiście prawdziwa, a wszystkie przekształcenia były równoważnościami, więc prawdziwa jest też wyjściowa nierówność.

Wersja PDF