Zadanie nr 5000598
Wykaż, że jeżeli ciąg 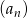 jest arytmetyczny, to ciąg
jest arytmetyczny, to ciąg 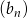 określony wzorem
określony wzorem 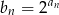 jest geometryczny.
jest geometryczny.
Rozwiązanie
Musimy sprawdzić, że iloraz dwóch kolejnych wyrazów ciągu 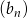 jest stały, tzn. że nie zależy od
jest stały, tzn. że nie zależy od  . Po drodze będziemy musieli skorzystać z tego, że ciąg
. Po drodze będziemy musieli skorzystać z tego, że ciąg 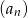 jest arytmetyczny, czyli
jest arytmetyczny, czyli 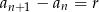 dla
dla 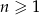 . Liczymy
. Liczymy
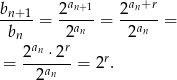
Wyrażenie to nie zależy od  , czyli ciąg
, czyli ciąg 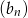 jest geometryczny.
jest geometryczny.

