/Szkoła średnia/Ciągi

Zadanie nr 5066006

Dodaj do ulubionych
Dodaj do rozwiązanych

W ciągu geometrycznym 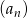(an) dane są iloraz 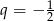1 q = − 2 oraz suma

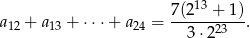
13 a12 + a13 + ⋅⋅⋅ + a24 = 7(2--+-1) . 3 ⋅223

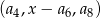Oblicz x , dla którego ciąg (a4,x − a6,a8) jest ciągiem arytmetycznym.

Rozwiązanie

Podana suma jest równa

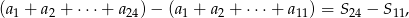
(a1 + a2 + ⋅⋅⋅+ a24) − (a1 + a2 + ⋅⋅⋅+ a11) = S 24 − S 11,

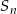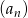gdzie Sn oznacza sumę n początkowych wyrazów ciągu (an) . Ze wzoru na 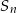Sn mamy równanie

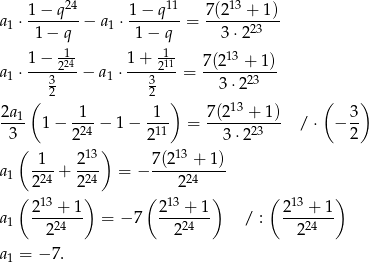
24 11 13 1-−-q-- 1-−-q-- 7(2--+--1) a 1 ⋅ 1 − q − a1 ⋅ 1 − q = 3⋅ 223 1-- -1- 1-−--224 1-+-211 7(2-13-+-1) a 1 ⋅ 3 − a1 ⋅ 3 = 3 ⋅223 ( 2 2 ) ( ) 2a1- -1- 1-- 7(213 +-1) 3- 3 1 − 2 24 − 1 − 211 = 3 ⋅223 / ⋅ − 2 ( 13) 13 a -1- + 2-- = − 7(2---+-1) 1 224 224 224 ( 13 ) ( 13 ) ( 13 ) a 1 2--+--1 = − 7 2---+-1 / : 2---+-1 224 224 224 a = − 7. 1

Zatem

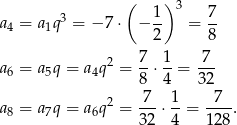
( ) 3 a4 = a1q3 = − 7 ⋅ − 1- = 7- 2 8 7 1 7 a6 = a5q = a4q2 = --⋅--= --- 8 4 32 a8 = a7q = a6q2 = 7--⋅ 1-= -7--. 32 4 128

Pozostało sprawdzić, kiedy liczby 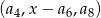(a4,x − a6,a8) są kolejnymi wyrazami ciągu arytmetycznego. Tak będzie, gdy

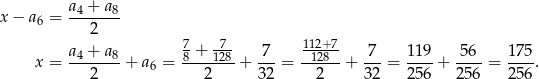
x − a6 = a4 +-a-8 2 a4 + a 8 7 + -7- 7 112+-7 7 119 56 175 x = -------+ a6 = 8---128-+ --- = --128--+ ---= ----+ ----= ---. 2 2 3 2 2 32 256 256 256

 
Odpowiedź: x = 175 256

Wersja PDF