/Szkoła średnia/Ciągi

Zadanie nr 5066666

Dodaj do ulubionych
Dodaj do rozwiązanych

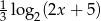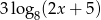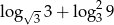Wyznacz liczbę x , tak aby liczby dodatnie: 1 3 log 2(2x + 5) , 3 lo g8(2x + 5) , lo g√3 3+ lo g239 tworzyły ciąg geometryczny.

Rozwiązanie

Ze względu na dziedzinę logarytmu musi oczywiście być 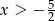5 x > − 2 .

Trzy liczby tworzą ciąg geometryczny jeżeli kwadrat środkowej jest iloczynem liczb sąsiednich. Musimy więc rozwiązać równanie.

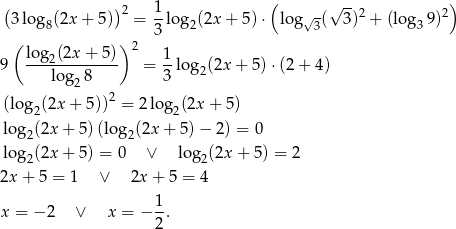
( -- ) (3 lo g (2x + 5))2 = 1log (2x + 5)⋅ lo g√-(√ 3 )2 + (log 9)2 8 3 2 3 3 ( log (2x + 5 )) 2 1 9 ---2--------- = --lo g2(2x + 5) ⋅(2+ 4) log 28 3 2 (log2(2x + 5)) = 2log2(2x + 5 ) log2(2x + 5) (lo g2(2x + 5) − 2) = 0 log (2x + 5) = 0 ∨ log (2x + 5) = 2 2 2 2x+ 5 = 1 ∨ 2x + 5 = 4 1 x = − 2 ∨ x = − -. 2

Pierwsze rozwiązanie odrzucamy, bo wyrazy ciągu mają być dodatnie.  
Odpowiedź: x = − 1 2

Wersja PDF