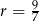/Szkoła średnia/Ciągi

Zadanie nr 5088628

Dodaj do ulubionych
Dodaj do rozwiązanych

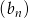Liczba 3 4 jest pierwszym wyrazem ciągu geometrycznego (bn) , którego iloraz jest równy 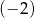(− 2) . Pierwszy wyraz ciągu arytmetycznego 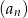(an) jest taki sam jak pierwszy wyraz ciągu 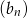(bn) . Suma siedmiu początkowych wyrazów ciągu 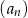(an) jest równa sumie siedmiu początkowych wyrazów ciągu 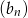(bn) . Oblicz różnicę ciągu arytmetycznego (an) .

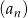Rozwiązanie

Skoro znamy pierwszy wyraz i iloraz ciągu 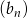(bn ) , to możemy obliczyć sumę siedmiu początkowych wyrazów ciągu (bn ) .

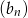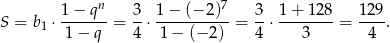
n 7 S = b ⋅ 1−--q--= 3-⋅ 1−--(−2-)-= 3-⋅ 1-+-12-8 = 1-29. 1 1 − q 4 1 − (− 2) 4 3 4

Zatem ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy równanie

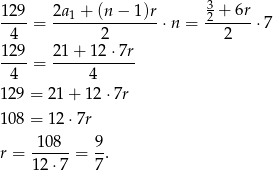
129 2a1 + (n− 1)r 3+ 6r ----= --------------⋅ n = -2-----⋅7 4 2 2 129-= 21+--12⋅-7r- 4 4 12 9 = 21 + 12 ⋅7r 10 8 = 12 ⋅7r -108-- 9- r = 12⋅ 7 = 7 .

 
Odpowiedź: r = 9 7

Wersja PDF