Zadanie nr 5181816
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 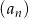 wyraża się wzorem
wyraża się wzorem 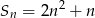 dla
dla 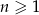 .
.
- Oblicz sumę 50 początkowych wyrazów tego ciągu o numerach parzystych:
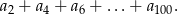
- Oblicz
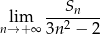
Rozwiązanie
- Ponieważ
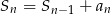 , to
, to 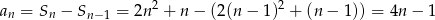
Zauważmy teraz, że ciąg
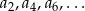 jest również ciągiem arytmetycznym, ale o różnicy dwa razy większej niż różnica ciągu
jest również ciągiem arytmetycznym, ale o różnicy dwa razy większej niż różnica ciągu 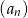 . Możemy zatem skorzystać ze wzoru na
. Możemy zatem skorzystać ze wzoru na 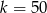 początkowych wyrazów ciągu arytmetycznego (korzystamy z najprostszej do zapamiętania postaci tego wzoru: (pierwszy+ostatni)/2 razy liczba wyrazów)
początkowych wyrazów ciągu arytmetycznego (korzystamy z najprostszej do zapamiętania postaci tego wzoru: (pierwszy+ostatni)/2 razy liczba wyrazów) 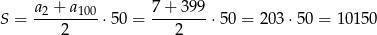
Odpowiedź: 10150 - Korzystamy ze wzoru na
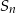 z treści zadania
z treści zadania 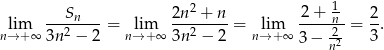
Odpowiedź: