/Szkoła średnia/Ciągi

Zadanie nr 5276830

Dodaj do ulubionych
Dodaj do rozwiązanych

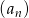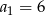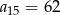Oblicz sumę pierwszych 14 wyrazów ciągu arytmetycznego (an) jeżeli a1 = 6 oraz a15 = 62 .

Rozwiązanie

Sposób I

Będziemy korzystać ze wzoru

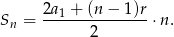
2a + (n − 1)r Sn = --1------------⋅n. 2

Mamy 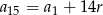a15 = a1 + 14r , czyli

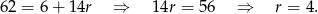
62 = 6+ 14r ⇒ 14r = 5 6 ⇒ r = 4.

Zatem

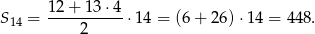
12 + 13 ⋅4 S 14 = -----------⋅14 = (6 + 26 )⋅14 = 448. 2

Sposób II

Korzystając z podanych danych łatwo obliczyć sumę pierwszych 15 wyrazów ciągu 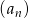(an) .

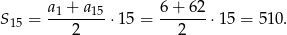
S = a1 +-a15⋅1 5 = 6-+-62-⋅15 = 510. 15 2 2

Suma pierwszych 14 wyrazów jest więc równa

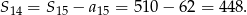
S14 = S 15 − a15 = 51 0− 6 2 = 448.

 
Odpowiedź: 448

Wersja PDF