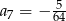Zadanie nr 5318038
W ciągu geometrycznym 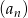 dane są iloraz
dane są iloraz 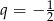 oraz suma
oraz suma
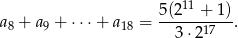
Oblicz 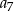 .
.
Rozwiązanie
Podana suma jest równa
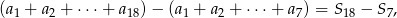
gdzie 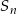 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 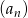 . Ze wzoru na
. Ze wzoru na 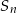 mamy równanie
mamy równanie
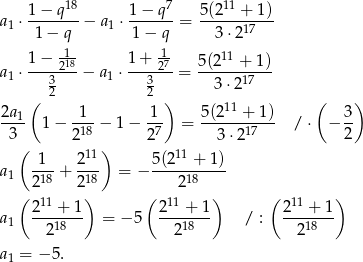
Zatem
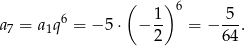
Odpowiedź: 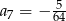
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W ciągu geometrycznym 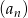 dane są iloraz
dane są iloraz 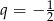 oraz suma
oraz suma
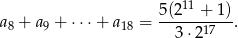
Oblicz 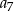 .
.
Podana suma jest równa
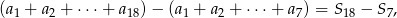
gdzie 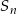 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 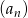 . Ze wzoru na
. Ze wzoru na 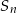 mamy równanie
mamy równanie
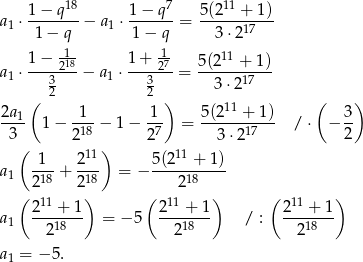
Zatem
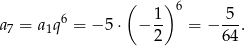
Odpowiedź: