Zadanie nr 5380740
W nieskończonym rosnącym ciągu geometrycznym 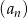 o wyrazach dodatnich, określonym dla
o wyrazach dodatnich, określonym dla 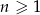 , stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy
, stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy 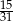 , a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy
, a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy 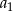 i
i 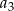 ciągu
ciągu 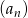 , są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego
, są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego 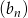 . Oblicz sumę 10 początkowych wyrazów ciągu
. Oblicz sumę 10 początkowych wyrazów ciągu 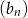 .
.
Uwaga: średnia geometryczna liczb 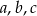 jest równa
jest równa 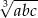 .
.
Rozwiązanie
Jeżeli oznaczymy przez 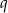 iloraz ciągu geometrycznego
iloraz ciągu geometrycznego 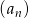 , to wiemy, że
, to wiemy, że
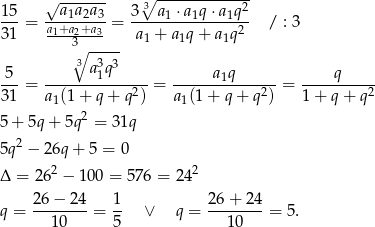
Ponieważ ciąg ma być rosnący i dodatni mamy stąd 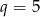 i z podanej sumy 4 pierwszych wyrazów otrzymujemy
i z podanej sumy 4 pierwszych wyrazów otrzymujemy
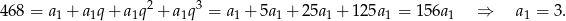
Wiemy, że w ciągu arytmetycznym 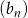 mamy
mamy
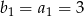
oraz
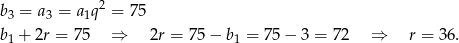
Pozostało teraz obliczyć sumę 10 początkowych wyrazów ciągu 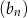 .
.
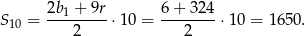
Odpowiedź: 1650

