/Szkoła średnia/Ciągi

Zadanie nr 5423465

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg arytmetyczny 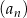(an ) określony dla każdej liczby naturalnej 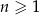n ≥ 1 , w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.

Rozwiązanie

Korzystamy ze wzoru

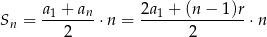
a + a 2a + (n − 1)r Sn = -1----n-⋅n = --1------------⋅n 2 2

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

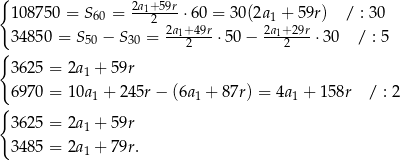
{ 2a1+59r 1087 50 = S60 = --2----⋅60 = 30 (2a 1 + 5 9r) / : 30 3485 0 = S50 − S30 = 2a1+49r⋅ 50− 2a1+-29r-⋅30 / : 5 { 2 2 3625 = 2a1 + 59r { 6970 = 10a1 + 245r − (6a1 + 87r) = 4a 1 + 1 58r / : 2 3625 = 2a + 59r 1 3485 = 2a1 + 79r.

Odejmujemy od drugiego równania pierwsze i mamy

20r = −1 40 ⇒ r = − 7.

Z drugiego równania

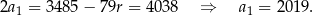
2a 1 = 3485 − 79r = 4 038 ⇒ a1 = 2 019.

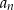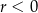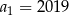Ponieważ ciąg an jest malejący (bo r < 0 ), więc jego największym wyrazem jest a1 = 2 019 .  
Odpowiedź: a1 = 2 019

Wersja PDF