/Szkoła średnia/Ciągi

Zadanie nr 5500653

Dodaj do ulubionych
Dodaj do rozwiązanych

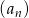Ciąg (an) jest określony rekurencyjnie w następujący sposób

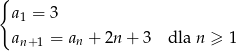
{ a1 = 3 an+1 = an + 2n + 3 dla n ≥ 1

Oblicz ile wyrazów tego ciągu jest mniejszych niż 2018.

Rozwiązanie

Zauważmy, że z podanego określenia ciągu

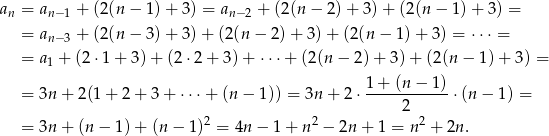
a = a + (2 (n− 1)+ 3) = a + (2(n − 2 )+ 3 )+ (2(n − 1)+ 3 ) = n n− 1 n−2 = an− 3 + (2 (n− 3)+ 3)+ (2(n− 2)+ 3)+ (2(n− 1)+ 3) = ⋅⋅⋅ = = a + (2 ⋅1+ 3)+ (2⋅2 + 3) + ⋅⋅⋅ + (2(n − 2) + 3) + (2(n − 1) + 3) = 1 1+--(n−--1)- = 3n + 2 (1+ 2+ 3 + ⋅ ⋅⋅+ (n − 1)) = 3n+ 2⋅ 2 ⋅(n − 1) = = 3n + (n − 1)+ (n − 1)2 = 4n − 1 + n2 − 2n + 1 = n2 + 2n.

Po drodze skorzystaliśmy ze wzoru 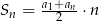Sn = a1+a2n-⋅n na sumę kolejnych wyrazów ciągu arytmetycznego. Pozostało teraz rozwiązać nierówność

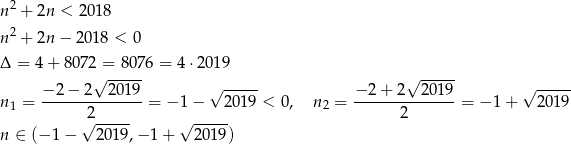
n2 + 2n < 2018 2 n + 2n − 201 8 < 0 Δ = 4+ 8072 = 80 76 = 4 ⋅2019 √ ----- √ ----- −2-−-2---2019- √ ----- −-2-+-2--20-19 √ ----- n1 = 2 = −1 − 2 019 < 0, n2 = 2 = − 1 + 201 9 √ ----- √ ----- n ∈ (− 1 − 2019 ,− 1 + 20 19)

Ponieważ 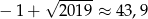√ ----- − 1 + 201 9 ≈ 43,9 , pierwsze 43 wyrazy ciągu 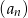(an) są mniejsze od 2018.  
Odpowiedź: 43

Wersja PDF