/Szkoła średnia/Ciągi

Zadanie nr 5585072

Dodaj do ulubionych
Dodaj do rozwiązanych

Na wykresie funkcji 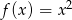2 f(x ) = x wybrano trzy różne punkty, których odcięte są kolejnymi wyrazami ciągu arytmetycznego, a rzędne kolejnymi wyrazami ciągu geometrycznego. Wykaż, że odcięta co najmniej jednego z tych punktów jest liczbą niewymierną.

Rozwiązanie

Kawałek z wykresem funkcji służy tylko zaciemnieniu tego, o co chodzi w zadaniu: mamy trzy liczby

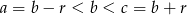
a = b − r < b < c = b+ r

tworzące ciąg arytmetyczny, takie, że 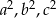a2,b2,c2 tworzą ciąg geometryczny (rzędna punktu na wykresie funkcji to po prostu wartość funkcji). Fakt, że liczby 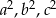a2,b2,c2 tworzą ciąg geometryczny oznacza, że

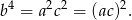
b4 = a2c2 = (ac)2.

Mamy dwie mozliwości

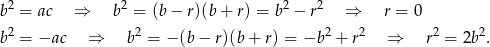
b 2 = ac ⇒ b2 = (b − r)(b + r) = b2 − r2 ⇒ r = 0 2 2 2 2 2 2 b = −ac ⇒ b = − (b − r)(b+ r) = −b + r ⇒ r = 2b .

Pierwsza sytuacja jest sprzeczna z treścią zadania (liczby 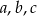a,b,c są wtedy równe), a druga oznacza, że

r √ -- b-= ± 2 .

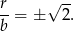
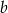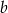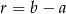Widać więc, że liczby r i b nie mogą być jednocześnie wymierne, a więc a i b też nie mogą być jednocześnie wymierne (bo r = b − a ).

Wersja PDF