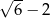Zadanie nr 5673867
Oblicz sumę nieskończonego szeregu geometrycznego
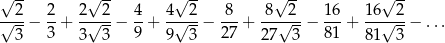
Rozwiązanie
Szereg, z którym mamy do czynienia to szereg geometryczny z pierwszym wyrazem 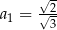 i ilorazem
i ilorazem 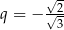 . Jego suma jest więc równa
. Jego suma jest więc równa
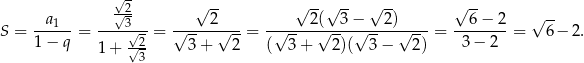
Odpowiedź: 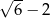
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz sumę nieskończonego szeregu geometrycznego
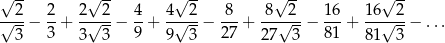
Szereg, z którym mamy do czynienia to szereg geometryczny z pierwszym wyrazem 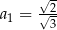 i ilorazem
i ilorazem 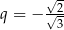 . Jego suma jest więc równa
. Jego suma jest więc równa
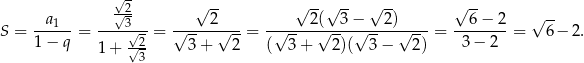
Odpowiedź: