/Szkoła średnia/Ciągi

Zadanie nr 5854343

Dodaj do ulubionych
Dodaj do rozwiązanych

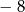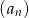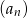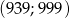Liczby − 8 i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego (an) . Oblicz ile wyrazów ciągu (an) należy do przedziału (93 9;999) .

Rozwiązanie

Skoro znamy dwa kolejne wyrazy ciągu arytmetycznego, to łatwo obliczyć różnicę tego ciągu

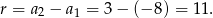
r = a 2 − a1 = 3− (−8 ) = 11.

Ze wzoru n -ty wyraz ciągu arytmetycznego mamy

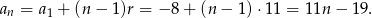
an = a1 + (n− 1)r = − 8 + (n − 1) ⋅11 = 11n − 19.

Pozostało teraz rozwiązać nierówność

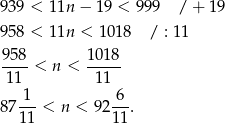
939 < 11n − 19 < 999 / + 19 958 < 11n < 1018 / : 11 958-< n < 1-018 1 1 11 1 6 87---< n < 92 --. 11 11

Ponieważ n jest liczbą naturalną, powyższą nierówność spełniają liczby

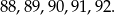
88,89 ,90,91,92.

Jest więc 5 takich liczb.  
Odpowiedź: 5 wyrazów

Wersja PDF