/Szkoła średnia/Ciągi

Zadanie nr 5855466

Dodaj do ulubionych
Dodaj do rozwiązanych

Iloraz ciągu geometrycznego 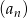(an) jest równy 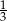1 3 , a suma jego pięciu początkowych wyrazów wynosi 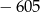− 60 5 . Znajdź pierwszy wyraz ciągu 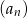(an ) oraz określ jego monotoniczność.

Rozwiązanie

Korzystamy ze wzoru na sumę n początkowych wyrazów ciągu geometrycznego

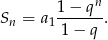
n Sn = a11-−-q--. 1 − q

W naszej sytuacji

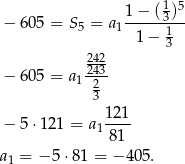
1 1-−-(3-)5 − 605 = S5 = a1 1− 1 3 224423 − 605 = a1-2-- 3 121- − 5 ⋅121 = a1 81 a1 = − 5 ⋅81 = −4 05.

Ponieważ pierwszy wyraz jest ujemny i iloraz jest mniejszy od 1, to każdy kolejny wyraz ciągu jest większy od poprzedniego (jest mniejszy co do wartości bezwzględnej, czyli ’mniej ujemny’). Ciąg jest zatem rosnący.  
Odpowiedź: 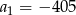a1 = − 40 5 , ciąg rosnący

Wersja PDF