/Szkoła średnia/Ciągi

Zadanie nr 5917492

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.

Rozwiązanie

Zaczynamy od rysunku

PIC

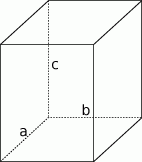
Z założeń otrzymujemy układ równań

{ a+ b+ c = 19 abc = 216

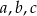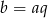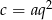Wiemy ponadto, że liczby a,b,c są kolejnymi wyrazami ciągu geometrycznego, czyli b = aq i c = aq2 dla pewnej liczby q ⁄= 0 .

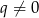Przekształćmy drugie równanie

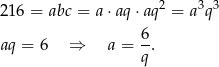
216 = abc = a ⋅aq⋅aq 2 = a3q3 6 aq = 6 ⇒ a = --. q

Wynik podstawiamy do pierwszego równania

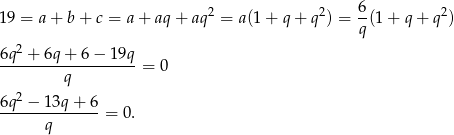
6 19 = a + b + c = a + aq + aq2 = a(1+ q+ q 2) = -(1 + q + q2) q 6q2 + 6q + 6 − 19q -------------------= 0 q 6q2-−-13q-+-6- q = 0.

Liczymy wyróżnik i pierwiastki

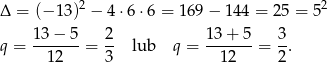
2 2 Δ = (− 13) − 4 ⋅6 ⋅6 = 169 − 14 4 = 25 = 5 13 − 5 2 13+ 5 3 q = --12---= 3- lub q = --12---= 2.

Zatem

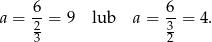
6- 6- a = 2 = 9 lub a = 3 = 4. 3 2

Teraz już łatwo obliczyć pole całkowite

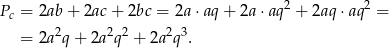
P = 2ab+ 2ac+ 2bc = 2a ⋅aq + 2a ⋅aq2 + 2aq ⋅aq2 = c = 2a2q+ 2a2q2 + 2a2q3.

Podstawiamy wyznaczone wartości

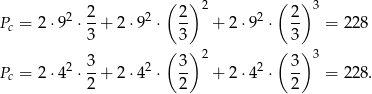
( ) ( ) 2 2 2 2 2 2 2 3 Pc = 2⋅9 ⋅--+ 2⋅9 ⋅ -- + 2⋅ 9 ⋅ -- = 228 3 ( 3) ( 3 ) 2 3 2 3 2 2 3 3 Pc = 2⋅4 ⋅2-+ 2⋅4 ⋅ 2- + 2⋅ 4 ⋅ 2- = 228.

 
Odpowiedź: Pc = 2 28

Wersja PDF