/Szkoła średnia/Ciągi

Zadanie nr 5982404

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozważmy ciąg trójkątów równobocznych takich, że długość boku pierwszego trójkąta jest równa a , zaś bok każdego następnego jest równy połowie wysokości poprzedniego. Oblicz sumę wszystkich pól tak utworzonych trójkątów.

Rozwiązanie

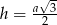Zobaczmy jak zmienia się pole, przy przejściu do kolejnego trójkata. Wysokość trójkąta równobocznego o boku a wyraża się wzorem √ - h = a--3 2 . Kolejny trójkąt ma mieć bok równy połowie tej wysokości czyli

√ -- a 3 ----. 4

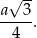
Jego pole jest równe

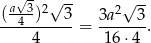
√- a-3-2√ -- 2√ -- (-4-)---3-= 3a---3-. 4 16 ⋅4

Pole wyjściowego trójkąta jest równe 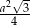a2√3 --4- , co daje nam iloraz

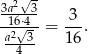
3a2√3 -16⋅4-- -3- a2√-3 = 16 . 4

Zatem ciąg pól tworzy ciąg geometryczny o pierwszym wyrazie równym 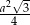a2√-3 4 i ilorazie 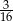316 . Suma takiego ciągu jest równa

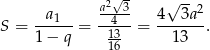
2√- √ -- a1 a-43 4 3a 2 S = ------= -13--= -------. 1 − q 16 13

 
Odpowiedź: √ -2 4-133a

Wersja PDF