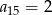/Szkoła średnia/Ciągi

Zadanie nr 6168596

Dodaj do ulubionych
Dodaj do rozwiązanych

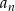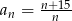Dany jest ciąg an o wyrazie ogólnym n+-15- an = n .

  • Oblicz, ile wyrazów ciągu 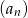(an) jest większych od 3.
  • Wyznacz wszystkie te wyrazy ciągu 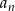an , które są liczbami naturalnymi.

Rozwiązanie

  • Musimy rozwiązać nierówność
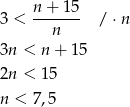
    3 < n-+-15- / ⋅n n 3n < n + 1 5 2n < 15 n < 7,5

     
    Odpowiedź: 7 pierwszych wyrazów

  • Przekształćmy wzór na wyraz ogólny ciągu
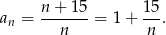
    n + 15 15 an = -------= 1+ --. n n

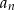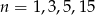    Widać teraz, że an jest liczbą naturalną tylko wtedy gdy n jest dzielnikiem 15, czyli dla n = 1 ,3,5,15 .  
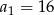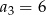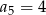    Odpowiedź: a = 16 1 , a = 6 3 , a5 = 4 , a15 = 2

Wersja PDF