Zadanie nr 6403470
Dany jest ciąg 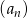 o wyrazie ogólnym
o wyrazie ogólnym 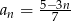 , dla
, dla 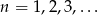 .
.
- Sprawdź, czy ciąg
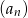 jest arytmetyczny.
jest arytmetyczny. - Oblicz, dla jakiej wartości
 liczby
liczby 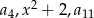 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Rozwiązanie
- Musimy sprawdzić czy różnica
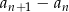 jest stała (nie zależy do
jest stała (nie zależy do  ). Liczymy
). Liczymy 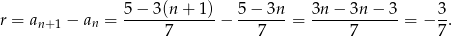
Zatem ciąg
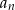 jest ciągiem arytmetycznym (o różnicy
jest ciągiem arytmetycznym (o różnicy 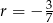 ).
). - Ponieważ
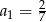 , mamy
, mamy 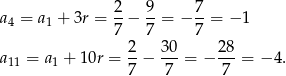
Zatem pytanie brzmi kiedy liczby
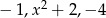 tworzą ciąg geometryczny. Tak będzie, gdy kwadrat środkowej będzie iloczynem pozostałych.
tworzą ciąg geometryczny. Tak będzie, gdy kwadrat środkowej będzie iloczynem pozostałych. 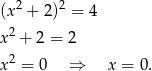
Opuszczając kwadrat w drugiej linijce skorzystaliśmy z tego, że
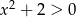 .
.
Odpowiedź: